La recherche de chemin, ou plus communément appelé "pathfinding" dans la sphère informatique (je m'en tiendrai d'ailleurs à ce mot pour la suite, désolé pour l'anglicisme mais c'est plus court ...) est un terme qui peut vous sembler obscure et pourtant vous l'utilisez tout les jours, dans la vie réelle ! Il s'agit en verité de la recherche du chemin le plus court pour aller d'un point A à un point B. Simple non ? Même s'il y a un mur il suffit de le contourner, mais en informatique, comment mettre ça en place ? On ne peut pas simplement demander au petit bonhomme "Allez hop, trouve le chemin tout seul !", tout doit être dicté.
C'est donc là qu'intervienne les différents algorithmes de recherche de chemin, chacun ayant des avantages et des défauts et donc une application précise, il n'existe pas d'algorithme ultime trouvant à cout sûr le meilleur chemin le plus rapidement possible ! Plongeons-nous dès à présent sur la première partie de ce qui constituera une série d'article sur le domaine du pathfinding.
Oh et ne vous en faite pas, comme pour les autres articles il n'y aura pas une seule ligne de code ou de math !


Posons déjà les bases du problème à résoudre: nous souhaitons trouver le chemin le plus court pour aller d'un point A à un point B, le tout en prenant le moins de temps possible (on n'a pas envie d'attendre une éternité avant la réponse !). Toutefois, il y a déjà un problème à résoudre en amont: de la même façon que nos yeux perçoivent les alentours, avec les differents obstacles, il va falloir les communiquer de la même façon à l'ordinateur.
Pour cela nous allons créer l'environnement informatique le plus simple qui soit, le quadrillage ! On appellera cette representation informatique d'un environnement, un maillage ou chaque case est representé par un "noeud" qui possède certaines propriétés.
De tous les cas de figure possible, le plus simple est bien sûr lorsqu'il n'y a pas d'obstacles entre notre point A et B, et le chemin le plus court est donc logiquement... ? Oui la ligne droite, bravo dans le fond ! Et ça heureusement, ce n'est pas très compliqué à faire même pour notre pauvre automate si on connaît les positions de chaque point.
Bon je ne vais pas vous mentir que la ligne droite, c'était un peu la question en chocolat car dès lors qu'on ajoute un obstacle là ça bloque ... Quelqu'un à une idée pour pouvoir avancer ? Non ? Bon, alors dans ce cas on n'a pas trop le choix: on va tester tous les chemins possible !
Et pour ça, nous allons utiliser l'aglorithme dit "Breadth First Search". Cet algorithme n'est pas limité au domaine du pathfinding et est d'ailleurs utilisé pour bien d'autres applications mais ici, c'est le B.A.-BA du pathfinding. Le principe est simple: on part d'une case, on test les cases voisines, on verifié si c'est un mur (auquel cas on abandonne le chemin) puis on enregistre le chemin et on passe aux cases suivante. N'hésitez pas à faire visualiser le processus pas à pas juste en dessous.
Cliquez n'importe où sur le quadrillage pour créer (ou effacer) un mur, et selectionnez les carrés rouge et noir pour pouvoir les bouger ! Le curseur permet de faire avancer l'algorithme de recherche pas à pas.
Et ... voilà, c'est tout ? Après tout, on a bien trouvé un chemin qui semble même être le plus rapide. Toutefois, bien que cet algorithme soit puissant il reste assez basique. En effet, considerons le cas de figure suivant: Jacque doit rejoindre Julie qui se trouve de l'autre coté de la rivière. Jacque pourrait passer par le pont mais il se trouve bien plus loin sur la rive ! Quel serait donc le chemin le plus rapide, traverser la rivière bien que ça le ralentirait fortement ou prendre le temps de faire un détour pour aller sur le pont ?
C'est là qu'entre en compte la notion de "coût" d'un chemin: en effet, chaque case va désormais avoir un coût plus ou moins important selon si on est sur de l'herbe, un marais ou bien une colline par exemple, la vitesse de passage est différente. Et vous l'aurez peut-être remarqué, mais "Breadth First" ne prend pas du tout en compte le coût d'un chemin.
Entre donc en scène Dijkstra ! (ouais pas facile à lire je sais) Quel est la différence ? Eh bien au lieu de choisir chaque chemin de la même façon, ces derniers seront désormais classés par ordre de priorité selon leur coût total. Ainsi lors de la recherche, l'algorithme va prioriser ceux qui ont le moindre coût et le chemin final ne sera donc plus celui le plus court en terme de distance, mais celui qui prend le moins de "temps" à parcourir (en verité, dans d'autre circonstance le coût d'un chemin pourrait representer autre chose que le temps de parcours).
Bien, donc on a réussi à trouver le chemin le plus court, et on a même pris en compte des situations particulière avec le coût des chemin, qu'y a-t-il d'autre à faire ? Eh bien, il y a un dernier facteur que nous n'avons pas encore vraiment pris en compte: le temps de calcul ! Eh oui, surtout si on doit faire ces calculs en temps réel ou pour pleins d'entités en même temps, il est primordial de minimiser le temps de calcul. Vous avez vous-même peut-être déjà remarqué qu'on effectuait une recherche de chemin derrière le point A, bien que le point B soit devant lui. Stupide non ? Il y a une part de verité, mais il est vrai qu'on peut encore optimiser le temps de calcul. Introduisons alors les fonctions heuristique !
Qu'est ce donc ? Simple: une fonction heuristique nous permet simplement de savoir à quel point nous sommes proche du point B (ici spatialement dans notre problème). Voyons tout de suite comment on peut l'implémenter. Sur un quadrillage, l'heuristique sera alors la distance à vol d'oiseau.
Tout comme Dijkstra permettait de prioriser les chemin ayant le chemin le moins couteux, "Greedy Best-First" est une autre variante de "Breadth First" qui priorise cette fois-ci les chemin les plus proche du point d'arrivé. Voyons comment il se débrouille par rapport Dijkstra (on revient sur un cas ou toutes les cases ont le même coût, mais ça ne change rien à la comparaison).
Oh pas mal ! Sur un environnement dénué d'obstacle, le chemin est trouvé presque immédiatement ! Mais ce n'est pas très interressant me direz-vous: en effet, si il n'y a pas d'obstacles, on peut tout simplement aller en ligne droite. Essayons maintenant de rajouter quelques obstacles ...
Et là on peut commencer à voir les différences entre les algorithmes. S'il n'y a pas trop d'obstacle, Greedy Best-First va bien trouver un chemin avant Dijkstra mais il n'est pas idéal. Dijkstra quant à lui fidèle à lui même va prendre un peu plus de temps mais réussira tout de même à trouver le meilleur chemin.
Comment faire pour fusionner l'efficacité de GBF et la fidelité de Dijkstra ? Ça serait le saint Graal, l'algorithme parfait ! Eh bien ne cherchez pas plus longtemps, il existe bel et bien et possède le doux nom de A* (à prononcer A-Star). Sans entrer dans les détails techniques, A* prend en compte le coût du chemin ET la distance à l'arrivée en bref le meilleur des deux mondes. Regardez plutôt:
A* trouve bien le chemin plus rapidement que Dijkstra et trouve tout de même le plus court en distance réel. En fait, A* est tellement efficace que ça reste le meilleur algorithme dans un environnement qui contient pas trop de mur. Mais qu'en est-il des cas particuliers ? Eh bien je vous ai déjà présenté le problème du cas ou il n'y a pas de murs: la ligne droite restera toujours la plus rapide et la meilleur des options, pas de doutes là dessus.
Et lorsqu'il y a beaucoup de murs, comme un labyrinthe par exemple ? C'est là que le bât blesse: les algorithmes prenant en compte la distance à l'objectif ne sont pas du tout avantagés car comme vous le savez, le meilleur chemin pour trouver la sortie d'un labyrinthe se trouve peut-être à son opposé. Dans ce genre de situation, ici Dijkstra restera peut-être le meilleur à moins de trouver un algorithme specifiquement dédié aux labyrinthes.
En fait, cela illustre bien le domaine de l'intelligence artificielle de manière générale: il n'y a pas de "meilleur algorithme", seulement des cas ou certains marcheront mieux que d'autres et à nous d'identifier ces situations et d'adapter notre petit automate.
On entre dans la dernière section de notre article que je considererais comme "bonus". Elle n'est pas essentiel à la compréhension mais je l'ai trouvé suffisement importante pour l'y inclure, en plus de vous donner des potentielles pistes de reflexion.
J'ai parlé plus haut de savoir identifier les différentes situations pour pouvoir y adapter notre algorithme. Ici, on ne va qu'en gratter la surface mais ça sera suffisant pour vous en donner un aperçu
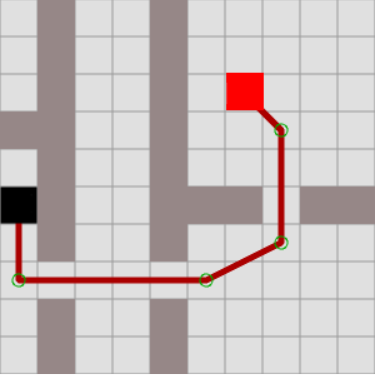
Nous en reparlerons plus tard dans la prochaine partie sur le pathfinding, mais vous avez peut-être remarqué que les chemin que nous avions faisaient parfois des sortes d'escalier au lieu de simplement aller en ligne droite. C'est une limitation du maillage en quadrillage, mais ça ne nous empêche pas d'essayer d'optimiser un peu le chemin !
Le principe est simple: pour chaque point du chemin, on va verifier si on peut avoir une ligne de vue direct vers les prochains point sans qu'il y ai d'obstacles. Si c'est la cas, alors on va en ligne droite vers le prochain point. Rien de plus simple !
Là aussi n'hésitez pas à dessiner ou effacer des murs et à bouger les 2 points. Vous pouvez activer la linéarisation et le déplacement automatique en cliquant sur les boutons !
Et voilà, on a un peu simplfié notre chemin ! On esquive bien les murs tout en prenant en ligne droite dans les espaces sans obstacles. Bien sûr cette optimisation de chemin reste ici limité et il y a bien d'autre manière de le faire, comme en passant par un maillage polygonal, mais nous verront cela dans un prochain article !
Si la lecture vous a interessé et que vous souhaiteriez en savoir plus dessus, je vous invite à lire le magnifique article de Red Blob Games sur le même sujet (dont j'ai tiré en grande partie le miens), page de blogs qui traite également d'autres sujets sur lesquels je suis particulièrement interessés et qui viendront sans doute prochainement.