Pour être honnête avec vous, la génération procedurale a toujours été un domaine qui m'a passioné dès que j'ai commencé à faire de l'informatique. Imaginez-vous à ma place quand j'étais encore petit: rentrer de l'école et sitôt le cartable jeté dans sur son lit, allumer en vitesse l'ordinateur familiale pour lancer une partie de votre jeu préféré "Minecraft". Voir un monde complet, infini et cohérents se créer sous vos yeux encore innocents, un monde total à explorer, toujours similaire et pourtant si différent à chaque fois.
Mais vous êtes-vous jamais demandé comment cela marchait ? Comment un "simple" code pouvait générer des mondes complètement cohérent, et qui ressemble au notre (oui bon, ça reste des cube mais nous nous sommes compris) ? En tout cas ça a été mon cas, et dès que j'ai découvert le merveilleux monde de la programmation et après avoir acquis des notions mathématiques suffisantes, je me suis rapidement penché dessus.
Bon néanmoins, aussi passionant soit le sujet (j'en ferai peut-être un blog dessus un de ces jours qui sait) ici nous allons parler des "bruit", communement appelé "Noise" en anglais, une des techniques permettant, entre autre, de générer ce genre de carte aléatoire.
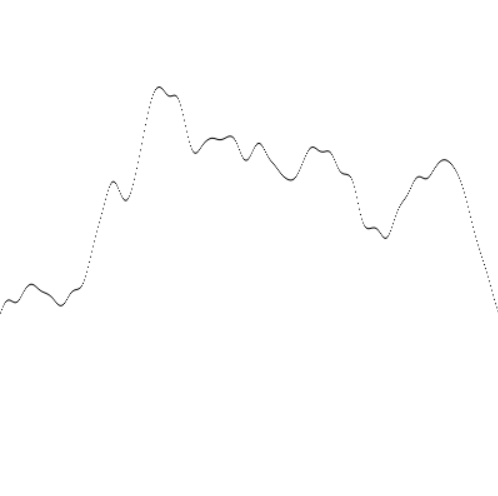


Alors oui je sais déjà ce que vous pensez: quel est le rapport entre du bruit et une magnifique map de Minecraft ? Déjà entendons-nous sur la signification du mot bruit: ici je ne parle pas du hurlement du bébé au restaurant vous brisant les oreilles ou de la douce mélodie émanant du marteau piqueur, je parle ici de sa signification plus générale. Un bruit est un signal parasite, une donnée indesirable qui perturbe l'analyse de notre environnement . Quelqu'un qui parle à coté de vous quand vous essayez de communiquer avec votre ami est un bruit. Le gresillement des écouteurs quand vous écoutez votre musique favorite est aussi un bruit. En soit, il n'est pas forcément dénué d'interêt, mais dans le cas présent il vous gène.
Et là je vous vois encore venir "Ok mais je ne vois toujours pas le rapport entre ça et Minecraft". Pas si vite, vous allez finir par comprendre (je l'espère) avant la fin de mon blog. mais retenez bien une chose on peut faire naître du chaos la plus belle des harmonies et ici ça sera bien le cas.
Bon alors, après 2 paragraphes de blabla introductifs on va enfin entrer dans le vif du sujet, je sais que vous n'en pouvez plus d'attendre. Fixons-nous l'objectif suivant: génerer une carte cohérente avec des creux, des plaines et des montagnes !
Tout d'abord comme expliqué tout à l'heure il va nous falloir créer des valeurs aléatoire, et quand je dis créer ce n'est pas avec une formule magique, on va le construire nous même avec des fonctions mathematiques relativement simple. Partons donc d'une sinusoïde, qui sera suffisante pour notre exemple.
Un sinus produit de jolies courbes, comme de belles collines. On peut faire varier leur taille en jouant sur la "fréquence" de la sinusoide ou bien leur amplitude. Testez sur le cadre ci-dessous !
Effectivement avec un peu d'imagination on peut y voir des collines, ou des montagnes selon votre humeur, mais tout cela semble bien lisse et un peu trop repetitif ce n'est pas du tout naturel ... N'y a-t-il point un moyen d'ajouter un peu de variation ? Eheh, c'est precisément là que ça devient interessant: pour faire varier nos jolies courbes, on va rajouter d'autres courbes par dessus, eh oui ! Mais attention, de fréquence et d'amplitude différentes evidemment, chacune déphasée l'une de l'autre.
Chaque couche suppplémentaire est appelé une octave et influe sur le "grain" de la courbe. Je vous laisse là encore experimenter sur le cadre ci-dessous pour bien vous rendre compte de l'influence des octaves sur notre bruit.
Bien maintenant que vous avez compris les bases de la génération d'un bruit on va pouvoir appliquer ça sur un plan 2D ce qui va être autrement plus interessant pour notre objectif final. Sur les exemples précédants nous avons utilisé une simple sinusoide comme base de notre bruit, mais cette fonction a ses limite. Toutefois, nous ne sommes pas limité à ça et d'ailleurs pour la suite nous allons utiliser ce qu'on appel un Bruit de Perlin (perlin's noise) ou sa version améliorée les Simplex Noise. Je ne vais pas vous détailler le fonctionnement d'un tel algorithme, mais retenez que vous allez obtenir des jolis gradients similaires au sinus mais de manière non périodique et applicable à plusieurs dimension facilement.
Là encore on peut influer sur sa fréquence ou son amplitude. On remarquera d'ailleurs qu'augmenter la fréquence tend un donner un effet de-zoom, et à très haute fréquence on obtiens un schéma ressemblant au "bruit blanc" des anciennes TV. Pour votre culture générale on qualifie par des couleurs les différents bruits: rouge pour les basses réquences, violet pour les très hautes fréquences et rose et bleu pour les entre-deux (blanc étant le juste milieu), chacun ayant des applications différentes. Toutefois, il est interessant de savoir que le cerveau interprête le bruit rouge comme "naturel" et est donc tout particulièrement adapté pour générer des reliefs.
Comment ? Si on peut aussi rajouter des octaves à notre bruit en 2D ? Mais bien sûr ! De manière général on peut dire que la fréquence influe sur le zoom du bruit tandis que les octaves quant à elles influent sur la précision. N'en abusons pas tout de même: plus vous mettez d'octave plus cela créer de couches à générer et donc augmente le temps de calcul. De plus vous l'avez peut-être déjà remarqué sur l'exemple linéaire mais ajouter trop d'octave devient inutile passé un certains stade (leur aplitude est negligeable) et peut avoir tendance à "applatir" la courbe. Certes on gagne du grain mais on perd également de plus en plus de vue nos grandes collines, tout finit par s'uniformiser, comme l'érosion sur une montagne.
Et maintenant, qu'est ce qu'il nous reste à faire ? Eh bien ... c'est tout. Notre bruit est là, il n'y a techniquement plus rien à faire. À vrai dire, il y a d'autres transformation que l'on peut faire sur notre bruit, pour accentuer les creux par exemple ou complètement transformer nos gradients mais je n'en parlerai pas ici.
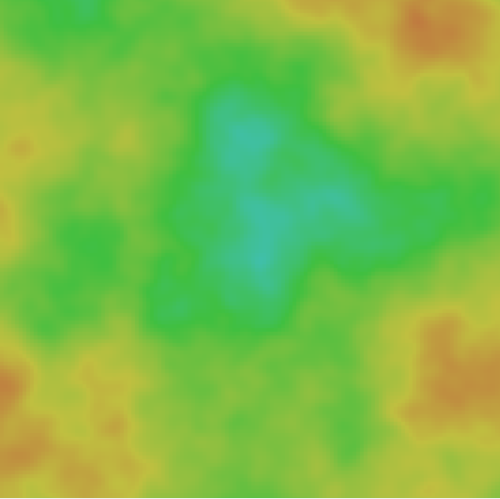
La seule chose qui nous reste à faire c'est de mettre en application ce magnifique bruit par diverses méthode. La plus intuitive serait de traiter directement le bruit 2D que nous avons comme un niveau d'altitude par exemple pour la transformer en carte comme montré ci-dessous, mais ce n'est pas la seule manière. J'ai pour cela mis en ligne quelques démos techniques de ce que l'on peut obtenir avec ces bruits, allant de la simple carte aléatoire à la simulation d'une nuée de billes en passant par des sortes de nuages évoluant dynamiquement. Chaque démo est agrémenté d'une petite explication technique de son fonctionnement pour les plus nerd d'entre vous, c'est pas génial ça ?
Si la lecture vous a interessé et que vous souhaiteriez en savoir plus dessus, je vous invite à lire le magnifique article de Red Blob Games sur le même sujet (dont j'ai tiré en grande partie le miens), page de blogs qui traite également d'autres sujets sur lesquels je suis particulièrement interessés et qui viendront sans doute prochainement.
Sinon, je vous mets aussi en lien d'autre articles plus techniques sur la symetrie cylindrique ou les Disques de Poisson qui interviennent dans mes démos techniques.